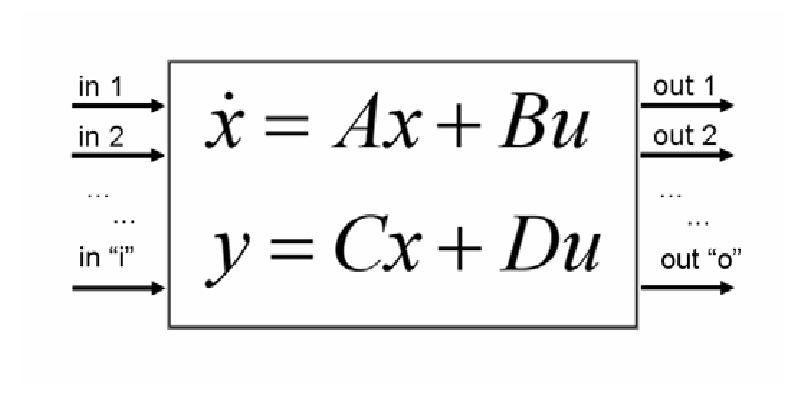modeling change
I’ve been thinking about how we model changes in dynamic systems. I know in mathematics this is a core idea of derivatives, but a few ideas I have not explored have been catching my eye lately. I wanted to take a short piece to go over some of the interesting ways that we model change in systems. They may include derivatives, but they sit perhaps a layer above derivatives. Using them as a critical tool.
State Space Models
Control engineering is a sub discipline focused on the control of devices that control other devices, primarily focused on algorithms used to drive a particular system into a desired state. In state space modeling, we model the inputs, the outputs, and the state variables in a system. We use this to see how different control parameters might influence our ability to generate particular behavior. The linear form of this equation takes the following form:
Here we are looking at two equations, the first derivative of the state vector, and the output vector. The first equation is broken down into the A matrix which represents how the current state x affects how the state should change. Th B vector represents how the input u should affect the state change. For the second equation, we have the C matrix representing how the state vector should affect the output, while we have the D matrix representing how the inputs should directly affect the output.
If we imagine this as a system, we might think of someone pushing a swing. The swing represents the variables of the system. The size of the cord, the weight of the swing, etc. Someone pushing that swing represents the inputs to that system, where by adding force to the mass of the swing, we make it swing back and forth. We use the first equation to model how the state variables, such as velocity and position, should change, and then the second equation to update them in our output. We might then feed these outputs back into the system to create a control loop. We can also say that each output is for a timestep, and thus created a time dependent state space model.
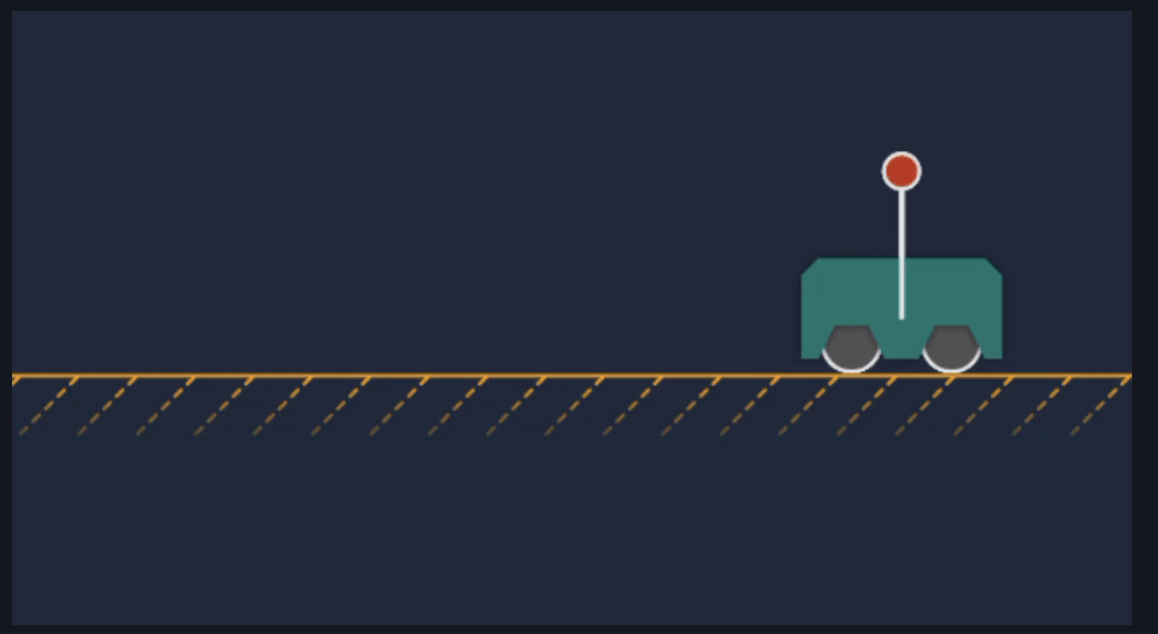
While writing this, a very cool visualization came out for state space models used in the single pole problem. I would definitely give it a look! It combied state space models with model predictive control to create an optimization function for putting a particul object into an ideal state. In this case, having a cart balance a pole.
Reinforcement Learning
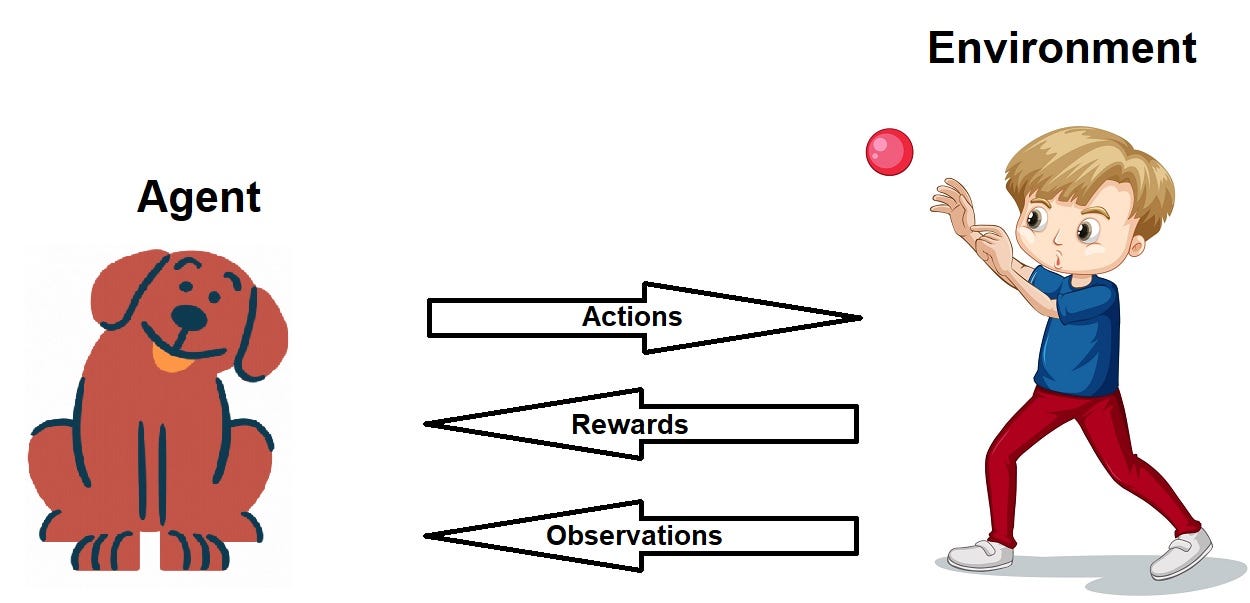
While not technically about modeling change in state, I think many of the ideas still apply, and I think it’s an interesting way to think about reinforcement learning. Reinforcement learning is generally about an agent attempting to make decisions in an environment to optimize some form of goal. We might think of this as a Markhov decision process, which is simply a process that uses no prior state information.
When we think about how agents change their state, we think about it in the context of their reward function. The reward function serves as a hueristic to determine whether the changes they are making are furthering a goal, or are hampering that goal. Most reinforcement learning comes down to environment design, and reward function design. We generally call the relationship between the agents actions and the expected reward to be the “policy” of the agent. If you’re interested in this, I would checkout OpenAI’s reinforcement learning package gymnasium.
What’s interesting is that there is nothing intrinsic in this policy document that states clearly how the environment should change. While in state space models we are modeling the changes in the environment, with reinforcement learning we are only modeling the decisions of the agent. However, the decisions of the agent clearly hold some knowledge about how the environment will change with respect to the reward function. If an agent figures out how to kick a soccer ball into a goal, then the agent must know, through its policy, what actions will have what effects on getting the soccer ball in the goal. Thus it does have some information on how the state will change with respect to its policy.
I’ll also add that in deep models, such as deep Q-learning, gradient descent is generally used. Gradient descent is based on momentum in physics, another idea deriving from the modeling of change in state. This however has to do with how the model weights should change, and not necessarily about how the state are the model will change.
Chaos Theory
Perhaps on a theoretical level, an area of physics deeply interested in the study of change is Chaos Theory. While an epic name, it’s just the study of systems whose output is highly sensitive to changes in input. Even systems that are deterministic can be affected, where the present state may determine the future state, but the approximate current state doesn’t determine the approximate future state. People may know about the butterfly affect, the double pendulum, or maybe the 3 body problem.
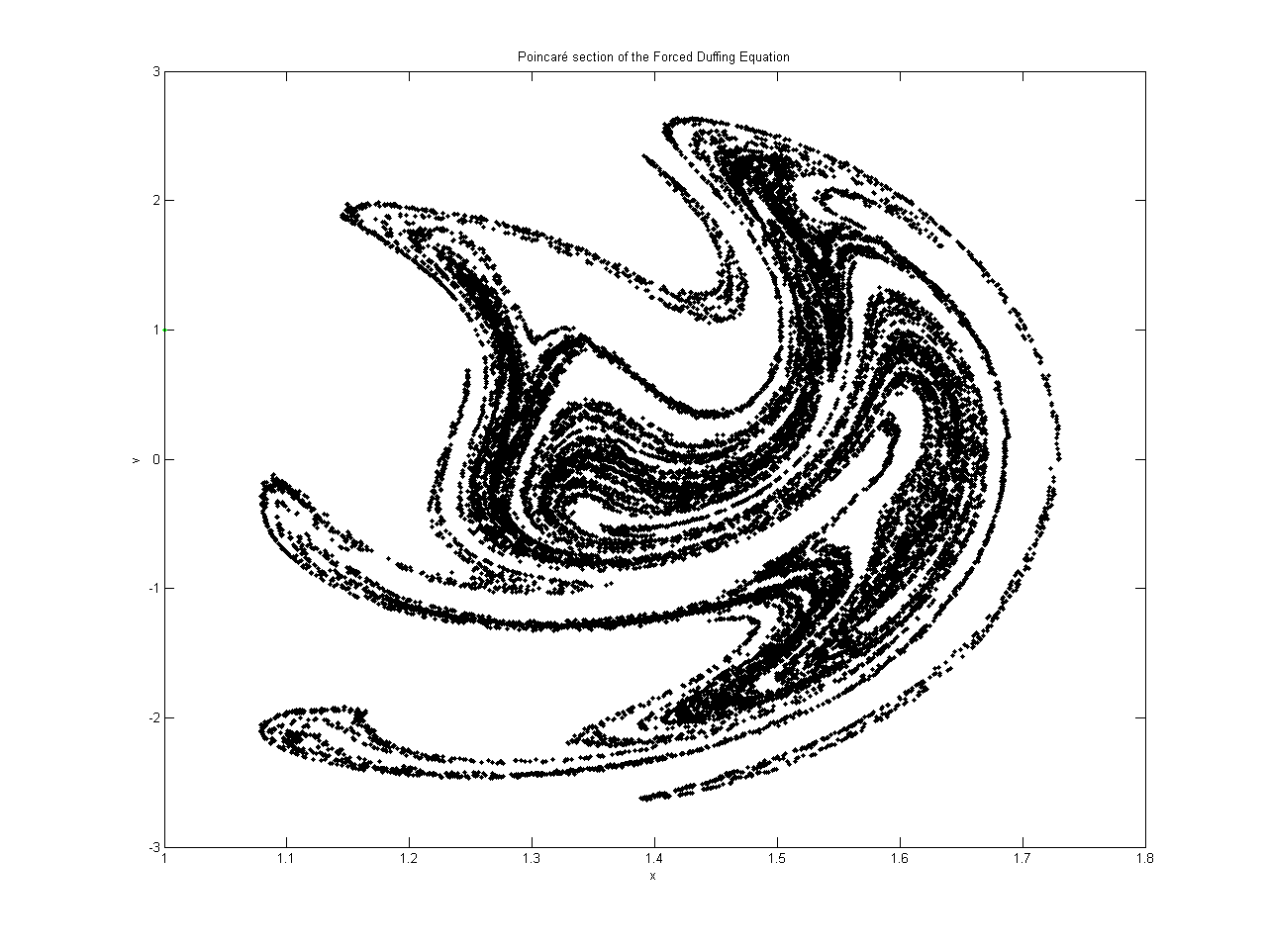
Much of choas theory has to do with attempting to find patterns in how systems change. For example, one might model the Poincaré map of the system, showcasing the frequency of the system to enter a particular state. Here we see each point represents a position in the Poincaré plane (the starting position) and where that value ended up when it returned through that plane. The hope is to find patterns in how these dynamic systems are changing.
Another good example is cellular automata. Many cellular automata can express chaotic behavior, depending on the rules of their setup. Stephan Wolfram recently wrote about it in his blog, but in short while the rules are clearly deterministic, it’s difficult to draw a relationship between the inputs and the output without calculating the result. This puts a cap on quickly solving problems. If we better understood exactly why these systems changed the way they did as a result of the input, we would be better able to grasp the connection.
Conclusion
While all of these examples can be construed as optimization problems, it’s interesting to focus on them not on how they model the desired end state, but in how they determine the change to get there. Differential equations are one of my favorite areas of math because of how applicable they are in different disciplines of science. These examples in physics, science, and engineering showcase that fact!